একটি সম্পূর্ণ চেইন এবং একটি শৃঙ্খলের একটি অংশের জন্য ওহমের আইন: সূত্র বিকল্প, বর্ণনা এবং ব্যাখ্যা

ক্লোজ সার্কিটের জন্য

ক্লোজড সার্কিট মানে একটি বন্ধ বৈদ্যুতিক সংযোগ যার মাধ্যমে কারেন্ট সঞ্চালিত হয়। যখন একে অপরের সাথে সংযোগকারী তারের একটি সিরিজ থাকে এবং সার্কিটটি সম্পূর্ণ করে যাতে আমি বৃত্তের এক প্রান্ত থেকে অন্য প্রান্তে চলে যাই, এটি একটি বন্ধ সার্কিট হবে।

EMF (E) - নির্দেশিত এবং ভোল্টে পরিমাপ করা হয় এবং ফ্যারাডে আইন অনুসারে ব্যাটারি বা চৌম্বক শক্তি দ্বারা উত্পন্ন ভোল্টেজকে বোঝায়, যা বলে যে একটি সময়-পরিবর্তিত চৌম্বক ক্ষেত্র একটি বৈদ্যুতিক প্রবাহকে প্ররোচিত করবে।

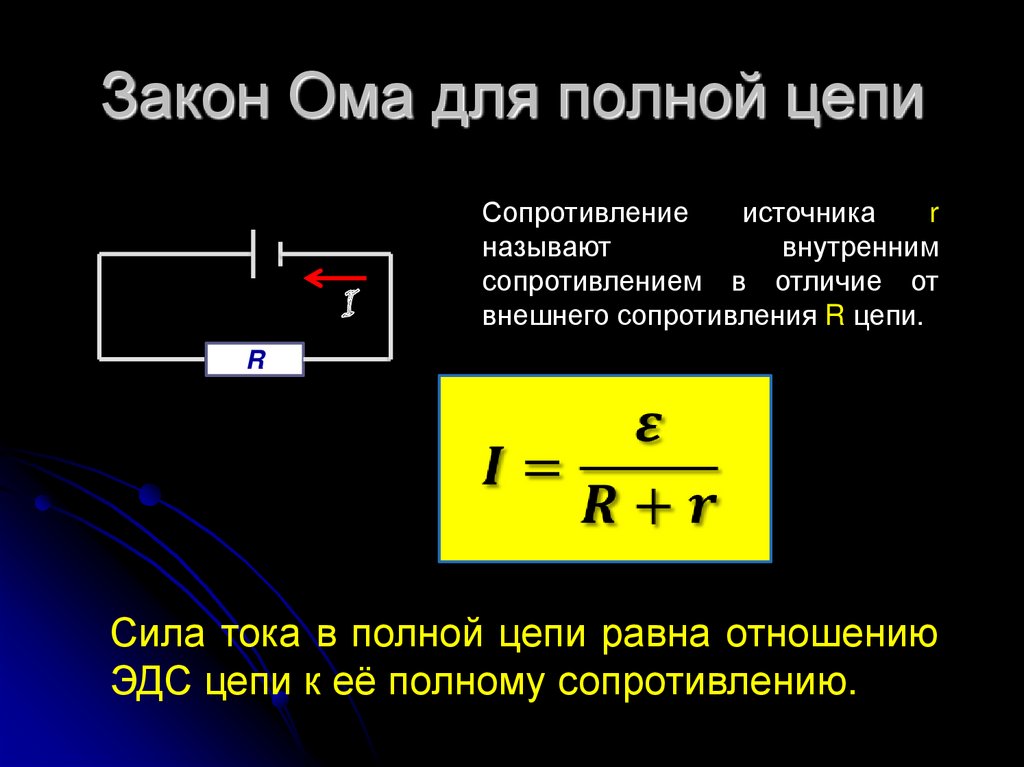
তারপর: E = IR + Ir

E \u003d I (R + r)

I \u003d E / (R + r)

যেখানে: r হল বর্তমান উৎসের রোধ।

এই অভিব্যক্তিটি বন্ধ লুপ সার্কিটের ওহমের সূত্র হিসাবে পরিচিত।

ভিন্নধর্মী চেইন

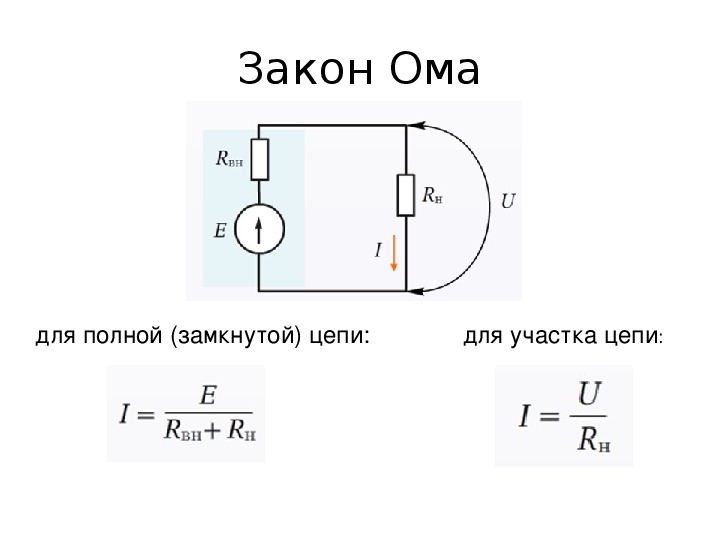
পৃথক বিভাগ এবং সম্পূর্ণ বৈদ্যুতিক সার্কিট

ওহমের সূত্র, একটি বিভাগ বা সমগ্র সার্কিটে প্রয়োগ করা হলে, দুটি গণনা বিকল্পে বিবেচনা করা যেতে পারে:

• পৃথক সংক্ষিপ্ত বিভাগ. এটি একটি EMF উৎস ছাড়া একটি সার্কিটের অংশ।
• এক বা একাধিক বিভাগ নিয়ে গঠিত একটি সম্পূর্ণ চেইন। এটির নিজস্ব অভ্যন্তরীণ প্রতিরোধের সাথে একটি EMF উত্সও অন্তর্ভুক্ত।

বৈদ্যুতিক সার্কিটের বর্তমান বিভাগের গণনা

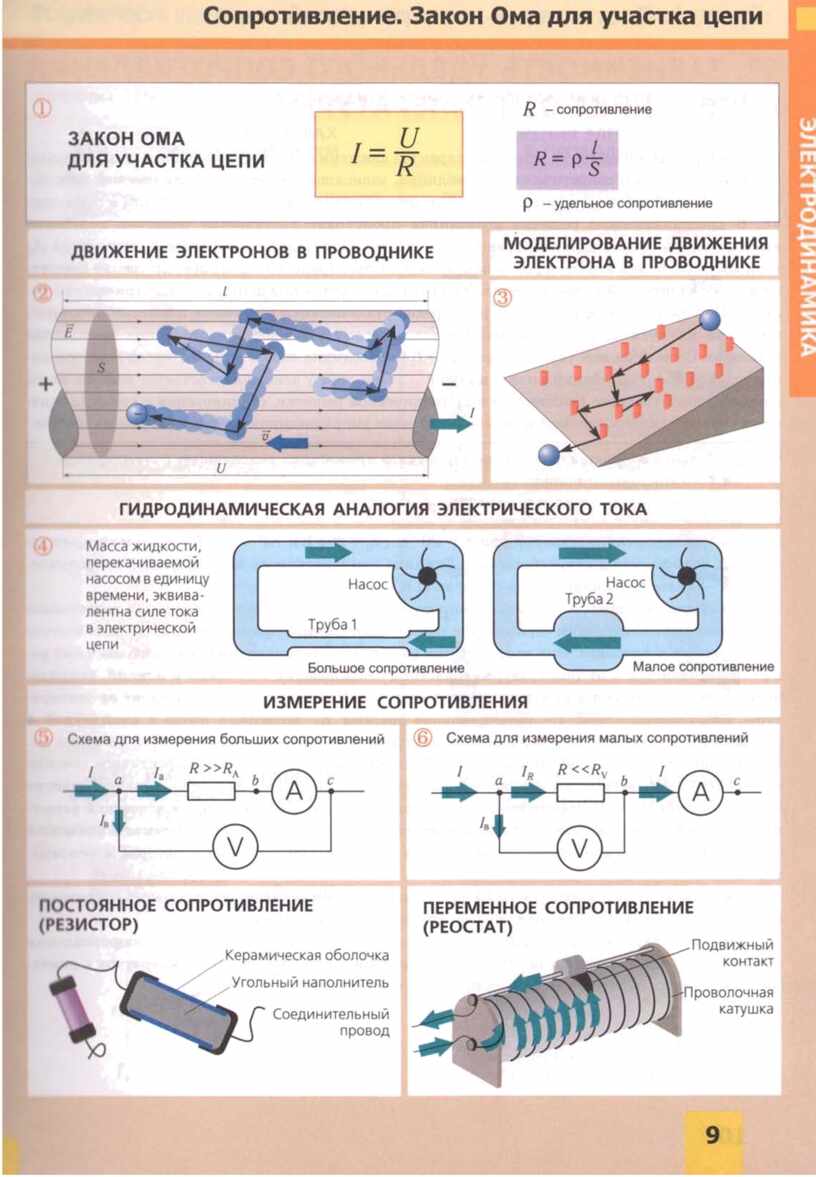
এই ক্ষেত্রে, মৌলিক সূত্র I \u003d U/R প্রয়োগ করা হয়, যার মধ্যে I হল বর্তমান শক্তি, U হল ভোল্টেজ, R হল প্রতিরোধ। এটি অনুসারে, কেউ ওহমের আইনের সাধারণভাবে গৃহীত ব্যাখ্যা প্রণয়ন করতে পারে:

এই সূত্রটি গ্রাফিক ডিজাইনে তথাকথিত "ক্যামোমাইল" উপস্থাপিত অন্যান্য অনেক সূত্রের ভিত্তি। P সেক্টরে - শক্তি নির্ধারণ করা হয়, সেক্টর I, U এবং R - বর্তমান শক্তি, ভোল্টেজ এবং প্রতিরোধের সাথে সম্পর্কিত ক্রিয়াগুলি সঞ্চালিত হয়।

প্রতিটি অভিব্যক্তি - মৌলিক এবং অতিরিক্ত উভয়ই আপনাকে সার্কিটে ব্যবহারের উদ্দেশ্যে উপাদানগুলির সঠিক পরামিতি গণনা করতে দেয়।

বৈদ্যুতিক সার্কিটগুলির সাথে কাজ করা বিশেষজ্ঞরা চিত্রে দেখানো ত্রিভুজ পদ্ধতি ব্যবহার করে যেকোন পরামিতিগুলির একটি দ্রুত সংকল্প সম্পাদন করেন।

গণনাগুলি বিভাগের উপাদানগুলির সাথে সংযোগকারী কন্ডাক্টরগুলির প্রতিরোধের বিবেচনায় নেওয়া উচিত। যেহেতু তারা বিভিন্ন উপকরণ থেকে তৈরি করা হয়, এই পরামিতি প্রতিটি ক্ষেত্রে ভিন্ন হবে।যদি একটি সম্পূর্ণ সার্কিট গঠনের প্রয়োজন হয়, তবে মূল সূত্রটি একটি ভোল্টেজ উত্সের পরামিতিগুলির সাথে সম্পূরক হয়, উদাহরণস্বরূপ, একটি ব্যাটারি।

একটি সম্পূর্ণ চেইন জন্য গণনা বিকল্প

একটি সম্পূর্ণ সার্কিট পৃথক বিভাগ নিয়ে গঠিত, যা একটি ভোল্টেজ সোর্স (EMF) সহ একটি একক সমগ্রের সাথে মিলিত হয়। এইভাবে, বিভাগগুলির বিদ্যমান প্রতিরোধকে সংযুক্ত উত্সের অভ্যন্তরীণ প্রতিরোধের দ্বারা সম্পূরক করা হয়। অতএব, পূর্বে আলোচিত মূল ব্যাখ্যাটি নিম্নরূপ পড়বে: I = U / (R + r)। এখানে, EMF উৎসের প্রতিরোধক সূচক (r) ইতিমধ্যেই যোগ করা হয়েছে।

বিশুদ্ধ পদার্থবিজ্ঞানের দৃষ্টিকোণ থেকে, এই সূচকটিকে খুব ছোট মান হিসাবে বিবেচনা করা হয়। যাইহোক, অনুশীলনে, জটিল সার্কিট এবং সার্কিট গণনা করার সময়, বিশেষজ্ঞরা এটিকে বিবেচনায় নিতে বাধ্য হন, যেহেতু অতিরিক্ত প্রতিরোধ কাজের নির্ভুলতাকে প্রভাবিত করে। উপরন্তু, প্রতিটি উত্সের গঠন খুব ভিন্ন, ফলস্বরূপ, কিছু ক্ষেত্রে প্রতিরোধ বেশ উচ্চ হার দ্বারা প্রকাশ করা যেতে পারে।

উপরের গণনাগুলি ডিসি সার্কিটের সাথে সম্পৃক্ত হয়। বিকল্প কারেন্ট সহ ক্রিয়া এবং গণনা একটি ভিন্ন স্কিম অনুযায়ী করা হয়।

একটি পরিবর্তনশীল উপর আইন প্রভাব

বিকল্প কারেন্টের সাথে, সার্কিটের প্রতিরোধ তথাকথিত প্রতিবন্ধকতা হবে, সক্রিয় প্রতিরোধ এবং প্রতিক্রিয়াশীল প্রতিরোধী লোড নিয়ে গঠিত। এটি ইন্ডাকটিভ বৈশিষ্ট্য এবং একটি সাইনোসয়েডাল বর্তমান মান সহ উপাদানগুলির উপস্থিতির কারণে। ভোল্টেজও একটি পরিবর্তনশীল, যা তার নিজস্ব সুইচিং আইন অনুযায়ী কাজ করে।

অতএব, ওহমের আইন এসি সার্কিট ডিজাইনটি নির্দিষ্ট প্রভাব বিবেচনায় নিয়ে গণনা করা হয়: ভোল্টেজ থেকে কারেন্টের পরিমানে অগ্রসর হওয়া বা পিছিয়ে থাকা, সেইসাথে সক্রিয় এবং প্রতিক্রিয়াশীল শক্তির উপস্থিতি।পালাক্রমে, প্রতিক্রিয়ার মধ্যে প্রবর্তক বা ক্যাপাসিটিভ উপাদান অন্তর্ভুক্ত থাকে।

এই সমস্ত ঘটনাগুলি Z \u003d U / I বা Z \u003d R + J * (XL - XC) সূত্রের সাথে মিলে যাবে, যার মধ্যে Z হল প্রতিবন্ধকতা; আর - সক্রিয় লোড; XL, XC - প্রবর্তক এবং ক্যাপাসিটিভ লোড; J হল সংশোধন কারক।

একটি সম্পূর্ণ সার্কিটে EMF উৎস

একটি বদ্ধ সার্কিটে বৈদ্যুতিক প্রবাহের ঘটনার জন্য, এই সার্কিটে কমপক্ষে একটি বিশেষ উপাদান থাকতে হবে যেখানে এর খুঁটির মধ্যে চার্জ স্থানান্তর করার কাজটি ঘটবে। যে শক্তিগুলি এই উপাদানটির ভিতরে চার্জ বহন করে তা বৈদ্যুতিক ক্ষেত্রের বিরুদ্ধে করে, যার মানে তাদের প্রকৃতি বৈদ্যুতিক থেকে আলাদা হতে হবে। অতএব, এই ধরনের শক্তিকে তৃতীয় পক্ষ বলা হয়।

ভাত। 1. পদার্থবিদ্যায় বাহ্যিক শক্তি।

বৈদ্যুতিক সার্কিটের একটি উপাদান যেখানে বাহ্যিক শক্তিগুলি বৈদ্যুতিক ক্ষেত্রের ক্রিয়াকলাপের বিরুদ্ধে চার্জ স্থানান্তর করতে কাজ করে তাকে কারেন্ট উত্স বলে। এর প্রধান বৈশিষ্ট্য হল বাহ্যিক শক্তির মাত্রা। এটিকে চিহ্নিত করার জন্য, একটি বিশেষ পরিমাপ চালু করা হয়েছে - ইলেক্ট্রোমোটিভ ফোর্স (EMF), এটি $\mathscr{E}$ অক্ষর দ্বারা চিহ্নিত করা হয়।

বর্তমান উৎসের EMF এর মান এই চার্জের মানের সাথে চার্জ স্থানান্তরের জন্য বাহ্যিক শক্তির অনুপাতের সমান:

$$\mathscr{E}={A_{st}\over q}$$

যেহেতু EMF এর অর্থ বৈদ্যুতিক ভোল্টেজের অর্থের খুব কাছাকাছি (রিকল, ভোল্টেজ হল বৈদ্যুতিক ক্ষেত্রের দ্বারা করা কাজের অনুপাত যা এই চার্জের মানের সাথে চার্জ বহন করে), তাই EMF, ভোল্টেজের মতো, পরিমাপ করা হয় ভোল্ট:

$$1B={J\overCl}$$

একটি বাস্তব তড়িৎ উৎসের দ্বিতীয় সবচেয়ে গুরুত্বপূর্ণ বৈদ্যুতিক বৈশিষ্ট্য হল এর অভ্যন্তরীণ প্রতিরোধ।যখন টার্মিনালগুলির মধ্যে চার্জ স্থানান্তরিত হয়, তখন তারা EMF উত্সের পদার্থের সাথে যোগাযোগ করে, এবং সেইজন্য, বৈদ্যুতিক প্রবাহের উত্সও কিছু প্রতিরোধ উপস্থাপন করে। অভ্যন্তরীণ প্রতিরোধ, সাধারণ প্রতিরোধের মতো, ওহমে পরিমাপ করা হয়, তবে ছোট ল্যাটিন অক্ষর $r$ দ্বারা চিহ্নিত করা হয়।

ভাত। 2. বর্তমান উৎসের উদাহরণ।

R - বৈদ্যুতিক প্রতিরোধের

রেজিস্ট্যান্স হল ভোল্টেজের পারস্পরিক এবং প্রবাহিত জলে নড়াচড়ার বিরুদ্ধে একটি দেহকে সরানোর প্রভাবের সাথে তুলনা করা যেতে পারে। R-এর একক হল ওম, যেটিকে গ্রীক অক্ষর ওমেগা দ্বারা চিহ্নিত করা হয়।

রেসিপ্রোকাল অফ রেজিস্ট্যান্স (1/R) পরিবাহিতা হিসাবে পরিচিত, যা একটি বস্তুর চার্জ পরিচালনা করার ক্ষমতা পরিমাপ করে, যা সিমেন্স ইউনিটে প্রকাশ করা হয়।

ব্যবহৃত জ্যামিতিকভাবে স্বাধীন পরিমাণকে রোধ বলা হয় এবং সাধারণত গ্রীক প্রতীক r দ্বারা চিহ্নিত করা হয়।

অতিরিক্ত তথ্য. ওহমের আইন বৈদ্যুতিক নেটওয়ার্কের অপারেশনের তিনটি গুরুত্বপূর্ণ সূচক স্থাপন করতে সাহায্য করে, যা শক্তির গণনাকে সহজ করে। এটি ডায়োড, ট্রানজিস্টর এবং এর মতো উপাদান সহ একতরফা নেটওয়ার্কের ক্ষেত্রে প্রযোজ্য নয়। এবং এটি অ-রৈখিক উপাদানগুলির ক্ষেত্রে প্রযোজ্য নয়, যার মধ্যে থাইরিস্টরগুলি উদাহরণ, যেহেতু এই উপাদানগুলির প্রতিরোধের মান বিভিন্ন প্রদত্ত ভোল্টেজ এবং কারেন্টের সাথে পরিবর্তিত হয়।

উচ্চ ফ্রিকোয়েন্সিতে, বিতরণ করা আচরণ প্রভাবশালী হয়ে ওঠে। একই জিনিস খুব দীর্ঘ পাওয়ার লাইনের সাথে ঘটে। এমনকি 60 Hz-এর মতো কম ফ্রিকোয়েন্সিতে, একটি খুব দীর্ঘ ট্রান্সমিশন লাইন, যেমন 30 কিমি, একটি বিতরণ প্রকৃতি আছে।প্রধান কারণ হল সার্কিটে প্রচারিত কার্যকর বৈদ্যুতিক সংকেতগুলি হল ইলেক্ট্রোম্যাগনেটিক তরঙ্গ, ভোল্ট এবং অ্যাম্পিয়ার নয়, যা একটি ইলেক্ট্রোম্যাগনেটিক তরঙ্গ দ্বারা সংক্রামিত হয়। কন্ডাক্টরগুলি কেবল তরঙ্গগুলির জন্য গাইড হিসাবে কাজ করে। সুতরাং, উদাহরণস্বরূপ, একটি সমাক্ষ তারের Z = 75 ohms দেখাবে, এমনকি যদি এর DC রোধ নগণ্য হয়।

ওহমের সূত্র বৈদ্যুতিক প্রকৌশলের মৌলিক আইন। এটির সমস্ত বৈদ্যুতিক সার্কিট এবং ইলেকট্রনিক উপাদানগুলিতে প্রচুর পরিমাণে ব্যবহারিক অ্যাপ্লিকেশন রয়েছে।

ওহমের আইন প্রয়োগের সবচেয়ে সাধারণ উদাহরণ:

1. বৈদ্যুতিক হিটারে বিদ্যুৎ সরবরাহ করা হয়। হিটার কয়েলের রেজিস্ট্যান্স এবং প্রয়োগকৃত ভোল্টেজের পরিপ্রেক্ষিতে, সেই হিটারে সরবরাহ করা শক্তি গণনা করা যেতে পারে।
2. ফিউজ পছন্দ. এগুলি সুরক্ষা উপাদান যা ইলেকট্রনিক ডিভাইসগুলির সাথে সিরিজে সংযুক্ত থাকে। ফিউজ/সিবিগুলিকে amps-এ রেট দেওয়া হয়। বর্তমান ফিউজ রেটিং ওহমের সূত্র ব্যবহার করে গণনা করা হয়।
3. ইলেকট্রনিক ডিভাইসের ডিজাইন। ইলেকট্রনিক ডিভাইস যেমন ল্যাপটপ এবং মোবাইল ফোনের জন্য একটি নির্দিষ্ট বর্তমান রেটিং সহ একটি ডিসি পাওয়ার সাপ্লাই প্রয়োজন। সাধারণ মোবাইল ফোনের ব্যাটারির জন্য 0.7-1A প্রয়োজন৷ এই উপাদানগুলির মধ্য দিয়ে প্রবাহিত কারেন্টের হার নিয়ন্ত্রণ করতে একটি প্রতিরোধক ব্যবহার করা হয়৷ একটি সাধারণ সার্কিটে রেট করা কারেন্ট গণনা করতে ওহমের সূত্র ব্যবহার করা হয়।

এক সময়ে, ওহমের উপসংহারগুলি বিদ্যুতের ক্ষেত্রে নতুন গবেষণার জন্য একটি অনুঘটক হয়ে ওঠে এবং আজ তারা তাদের তাত্পর্য হারায়নি, যেহেতু আধুনিক বৈদ্যুতিক প্রকৌশল তাদের উপর ভিত্তি করে। 1841 সালে, ওমকে রয়্যাল সোসাইটির সর্বোচ্চ সম্মান, কোপলি পদক প্রদান করা হয় এবং "ওম" শব্দটি 1872 সালের প্রথম দিকে প্রতিরোধের একক হিসাবে স্বীকৃত হয়।

ডিসি সার্কিটের অ-ইউনিফর্ম বিভাগ

একটি ভিন্নধর্মী কাঠামোর সার্কিটের এমন একটি অংশ রয়েছে, যেখানে কন্ডাক্টর এবং উপাদানগুলি ছাড়াও একটি বর্তমান উত্স রয়েছে। এই এলাকায় মোট বর্তমান শক্তি গণনা করার সময় এর EMF অবশ্যই বিবেচনায় নেওয়া উচিত।

একটি সূত্র রয়েছে যা একটি ভিন্নধর্মী সাইটের প্রধান পরামিতি এবং প্রক্রিয়াগুলিকে সংজ্ঞায়িত করে: q = q0 x n x V। এর সূচকগুলি নিম্নরূপ চিহ্নিত করা হয়েছে:

• চলন্ত চার্জ (q) প্রক্রিয়ায় তারা একটি নির্দিষ্ট ঘনত্ব অর্জন করে। এর কর্মক্ষমতা বর্তমান শক্তি এবং কন্ডাক্টর (এস) এর ক্রস-বিভাগীয় এলাকার উপর নির্ভর করে।
• একটি নির্দিষ্ট ঘনত্বের (n) অবস্থার অধীনে, একক সময়ের মধ্যে স্থানান্তরিত ইউনিট চার্জের সংখ্যা (q0) সঠিকভাবে নির্দেশ করা সম্ভব।
• গণনার জন্য, কন্ডাকটরকে শর্তসাপেক্ষে কিছু ভলিউম (V) সহ একটি নলাকার বিভাগ হিসাবে বিবেচনা করা হয়।

কন্ডাক্টরটিকে ব্যাটারির সাথে সংযুক্ত করার সময়, পরবর্তীটি কিছুক্ষণ পরে ডিসচার্জ করা হবে। অর্থাৎ, ইলেকট্রনের গতি ধীরে ধীরে কমে যায় এবং শেষ পর্যন্ত পুরোপুরি বন্ধ হয়ে যায়। এটি কন্ডাকটরের আণবিক জালি দ্বারা সহজতর হয়, যা একে অপরের সাথে ইলেক্ট্রনগুলির সংঘর্ষ এবং অন্যান্য কারণগুলির বিরুদ্ধে প্রতিরোধ করে। এই ধরনের প্রতিরোধকে অতিক্রম করার জন্য, নির্দিষ্ট তৃতীয় পক্ষের শক্তিগুলিকে অতিরিক্ত প্রয়োগ করতে হবে।

গণনার সময়, এই শক্তিগুলি কুলম্বের সাথে যোগ করা হয়। উপরন্তু, একটি ইউনিট চার্জ q 1ম বিন্দু থেকে 2য় স্থানান্তর করতে, এটি A1-2 বা সহজভাবে A12 কাজটি সম্পাদন করতে হবে। এই উদ্দেশ্যে, একটি সম্ভাব্য পার্থক্য (ϕ1 - ϕ2) তৈরি করা হয়। একটি সরাসরি বর্তমান উৎসের কর্মের অধীনে, একটি EMF উত্থিত হয়, সার্কিট বরাবর চার্জ চলমান। মোট চাপের মাত্রা উপরে উল্লিখিত সমস্ত শক্তির সমন্বয়ে গঠিত হবে।

ডিসি সরবরাহের সাথে সংযোগের পোলারিটি গণনাগুলিতে অবশ্যই বিবেচনায় নেওয়া উচিত। যখন টার্মিনালগুলি পরিবর্তন করা হয়, তখন EMFও পরিবর্তিত হবে, চার্জের চলাচলকে ত্বরান্বিত করবে বা ধীর করবে।

উপাদানগুলির সিরিয়াল এবং সমান্তরাল সংযোগ

একটি বৈদ্যুতিক সার্কিটের উপাদানগুলির জন্য (একটি সার্কিটের বিভাগ), একটি চরিত্রগত মুহূর্ত একটি সিরিজ বা সমান্তরাল সংযোগ।

তদনুসারে, প্রতিটি ধরণের সংযোগের সাথে বর্তমান প্রবাহ এবং ভোল্টেজ সরবরাহের একটি ভিন্ন প্রকৃতি রয়েছে। এই অ্যাকাউন্টে, ওহমের সূত্রটি বিভিন্ন উপায়ে প্রয়োগ করা হয়, উপাদানগুলি অন্তর্ভুক্ত করার বিকল্পের উপর নির্ভর করে।

সিরিজ-সংযুক্ত প্রতিরোধী উপাদানের একটি চেইন

একটি সিরিজ সংযোগের ক্ষেত্রে (দুটি উপাদান সহ একটি সার্কিটের বিভাগ), শব্দ ব্যবহার করা হয়:

• আমি = আমি₁ = আমি₂ ;
• উ = উ₁ + উ₂ ;
• আর = আর₁ + আর₂

এই সূত্রটি স্পষ্টভাবে দেখায় যে, সিরিজে সংযুক্ত প্রতিরোধক উপাদানের সংখ্যা নির্বিশেষে, সার্কিটের একটি বিভাগে প্রবাহিত কারেন্ট মান পরিবর্তন করে না।

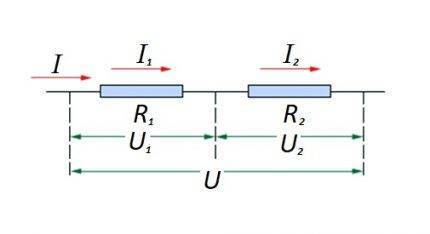একটি সার্কিট বিভাগে প্রতিরোধী উপাদানগুলিকে একে অপরের সাথে সিরিজে সংযুক্ত করা। এই বিকল্পটির নিজস্ব গণনা আইন রয়েছে। চিত্রে: I, I1, I2 - বর্তমান প্রবাহ; R1, R2 - প্রতিরোধী উপাদান; U, U1, U2 - প্রয়োগকৃত ভোল্টেজ

সার্কিটের সক্রিয় প্রতিরোধক উপাদানগুলিতে প্রয়োগ করা ভোল্টেজের পরিমাণ হল সমষ্টি এবং EMF উৎসের মান পর্যন্ত যোগ করে।

এই ক্ষেত্রে, প্রতিটি পৃথক উপাদানের ভোল্টেজ হল: Ux = I * Rx।

সার্কিটের সমস্ত প্রতিরোধক উপাদানের মানের সমষ্টি হিসাবে মোট প্রতিরোধকে বিবেচনা করা উচিত।

সমান্তরাল সংযুক্ত প্রতিরোধী উপাদানের একটি চেইন

ক্ষেত্রে যখন প্রতিরোধী উপাদানগুলির একটি সমান্তরাল সংযোগ থাকে, জার্মান পদার্থবিজ্ঞানী ওহমের আইনের সাপেক্ষে সূত্রটি ন্যায্য বলে বিবেচিত হয়:

• আমি = আমি₁ + আমি₂ … ;
• উ = উ₁ = উ₂ … ;
• 1/R = 1/R₁ + 1 / আর₂ + …

সমান্তরাল এবং সিরিয়াল সংযোগ ব্যবহার করা হলে একটি "মিশ্র" ধরনের সার্কিট বিভাগ কম্পাইল করার বিকল্পগুলি বাদ দেওয়া হয় না।

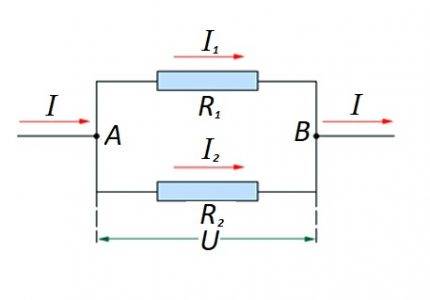একটি সার্কিট বিভাগে একটি আরেকটির সাথে সমান্তরালে প্রতিরোধী উপাদানগুলির সংযোগ। এই বিকল্পের জন্য, এর নিজস্ব গণনা আইন প্রয়োগ করা হয়। চিত্রে: I, I1, I2 - বর্তমান প্রবাহ; R1, R2 - প্রতিরোধী উপাদান; U - প্রয়োগ করা ভোল্টেজ; A, B - প্রবেশ/প্রস্থান পয়েন্ট

এই ধরনের বিকল্পগুলির জন্য, গণনা সাধারণত সমান্তরাল সংযোগের প্রতিরোধী রেটিং এর প্রাথমিক গণনা দ্বারা বাহিত হয়। তারপর সিরিজে সংযুক্ত রোধের মান ফলাফলে যোগ করা হয়।

আইনের অবিচ্ছেদ্য এবং ডিফারেনশিয়াল ফর্ম

গণনার সাথে উপরের সমস্ত পয়েন্টগুলি এমন পরিস্থিতিতে প্রযোজ্য যখন একটি "সমজাতীয়" কাঠামোর কন্ডাক্টর, তাই বলতে গেলে, বৈদ্যুতিক সার্কিটের অংশ হিসাবে ব্যবহৃত হয়।

এদিকে, অনুশীলনে, একজনকে প্রায়শই একটি পরিকল্পিত নির্মাণের সাথে মোকাবিলা করতে হয়, যেখানে কন্ডাক্টরগুলির গঠন বিভিন্ন এলাকায় পরিবর্তিত হয়। উদাহরণস্বরূপ, একটি বৃহত্তর ক্রস বিভাগের তারগুলি ব্যবহার করা হয় বা, বিপরীতভাবে, ছোটগুলি, বিভিন্ন উপকরণের ভিত্তিতে তৈরি।

এই জাতীয় পার্থক্যগুলি বিবেচনায় নেওয়ার জন্য, তথাকথিত "ডিফারেনশিয়াল-ইনটিগ্রাল ওহমের সূত্র" এর একটি ভিন্নতা রয়েছে। একটি অসীম ছোট কন্ডাক্টরের জন্য, বর্তমান ঘনত্বের স্তরটি তীব্রতা এবং পরিবাহিতা মানের উপর নির্ভর করে গণনা করা হয়।

ডিফারেনশিয়াল গণনার অধীনে, সূত্রটি নেওয়া হয়: J = ό * E

পূর্ণাঙ্গ গণনার জন্য, যথাক্রমে, সূত্র: I * R = φ1 - φ2 + έ

যাইহোক, এই উদাহরণগুলি উচ্চতর গণিতের স্কুলের কাছাকাছি এবং প্রকৃতপক্ষে একজন সাধারণ ইলেকট্রিশিয়ানের বাস্তব অনুশীলনে ব্যবহৃত হয় না।

বর্তমান এবং প্রতিরোধের বোঝা

তড়িৎ প্রবাহের ধারণা দিয়ে শুরু করা যাক।সংক্ষেপে, ধাতুর সাথে বৈদ্যুতিক প্রবাহ হল ইলেকট্রনের নির্দেশিত গতিবিধি - নেতিবাচক চার্জযুক্ত কণা। এগুলি সাধারণত ছোট বৃত্ত হিসাবে উপস্থাপিত হয়। একটি শান্ত অবস্থায়, তারা বিশৃঙ্খলভাবে সরে যায়, ক্রমাগত তাদের দিক পরিবর্তন করে। কিছু নির্দিষ্ট অবস্থার অধীনে - একটি সম্ভাব্য পার্থক্যের চেহারা - এই কণাগুলি কিছু দিকে একটি নির্দিষ্ট আন্দোলন শুরু করে। এই আন্দোলন হল বৈদ্যুতিক প্রবাহ।

এটি পরিষ্কার করার জন্য, আমরা কিছু সমতলে ছড়িয়ে পড়া জলের সাথে ইলেকট্রন তুলনা করতে পারি। যতক্ষণ বিমানটি স্থির থাকে, ততক্ষণ জল সরে না। কিন্তু, যত তাড়াতাড়ি একটি ঢাল উপস্থিত হয় (একটি সম্ভাব্য পার্থক্য দেখা দেয়), জল সরানো শুরু করে। ইলেক্ট্রনের ক্ষেত্রেও তাই।

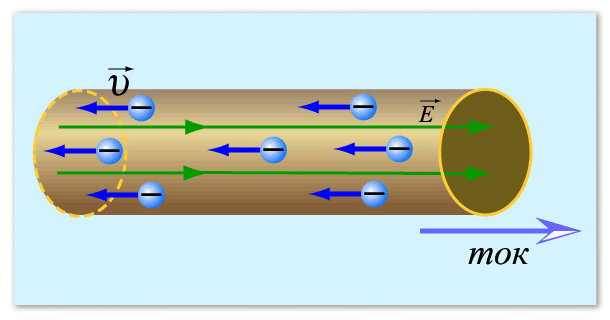
এভাবেই বৈদ্যুতিক প্রবাহ কল্পনা করা যায়

এখন আমাদের বুঝতে হবে প্রতিরোধ কী এবং কেন তাদের বর্তমান শক্তির সাথে প্রতিক্রিয়া রয়েছে: প্রতিরোধ যত বেশি হবে, স্রোত তত কম হবে। আপনি জানেন, ইলেকট্রন একটি পরিবাহীর মধ্য দিয়ে চলে। সাধারণত এগুলি ধাতব তার, যেহেতু ধাতুগুলির বিদ্যুৎ সঞ্চালনের ক্ষমতা ভাল। আমরা জানি যে ধাতুটির একটি ঘন স্ফটিক জালি রয়েছে: অনেকগুলি কণা যা কাছাকাছি এবং আন্তঃসংযুক্ত। ইলেকট্রন, ধাতব পরমাণুর মধ্যে তাদের পথ তৈরি করে, তাদের সাথে সংঘর্ষ হয়, যা তাদের পক্ষে সরানো কঠিন করে তোলে। এটি একটি পরিবাহী যে প্রতিরোধের প্রয়োগ করে তা চিত্রিত করতে সাহায্য করে। এখন এটা পরিষ্কার হয়ে গেছে কেন প্রতিরোধ ক্ষমতা যত বেশি, বর্তমান শক্তি তত কম - যত বেশি কণা, ইলেক্ট্রনদের পক্ষে পথ অতিক্রম করা তত বেশি কঠিন, তারা এটি আরও ধীরে ধীরে করে। এটা সাজানো হয়েছে মনে হয়.

আপনার যদি এই নির্ভরতা পরীক্ষামূলকভাবে পরীক্ষা করার ইচ্ছা থাকে তবে একটি পরিবর্তনশীল প্রতিরোধক খুঁজুন, সিরিজে একটি প্রতিরোধক - একটি অ্যামিটার - একটি বর্তমান উত্স (ব্যাটারি) সংযুক্ত করুন।সার্কিটে একটি সুইচ ঢোকানোও বাঞ্ছনীয় - একটি সাধারণ টগল সুইচ।

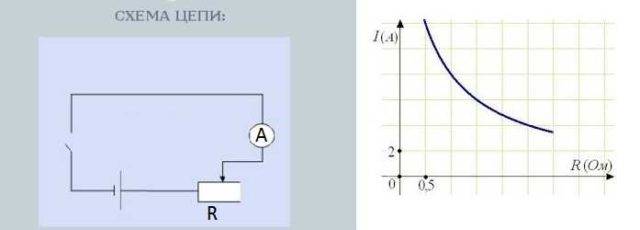
প্রতিরোধের উপর বর্তমানের নির্ভরতা পরীক্ষার জন্য সার্কিট

রোধের গাঁট ঘুরিয়ে দিলে প্রতিরোধের পরিবর্তন হয়। একই সময়ে, অ্যামিটারের রিডিং, যা বর্তমান শক্তি পরিমাপ করে, এছাড়াও পরিবর্তন হয়। তদুপরি, প্রতিরোধ যত বেশি হবে, তীরটি তত কম বিচ্যুত হবে - কম স্রোত। প্রতিরোধ যত কম হবে তীরটি তত বেশি বিচ্যুত হবে - স্রোত তত বেশি।

প্রতিরোধের উপর বর্তমানের নির্ভরতা প্রায় রৈখিক, অর্থাৎ, এটি প্রায় সরল রেখা হিসাবে গ্রাফে প্রতিফলিত হয়। কেন প্রায় - এই আলাদাভাবে আলোচনা করা উচিত, কিন্তু যে অন্য গল্প.

বিকল্প স্রোতের জন্য ওহমের সূত্র

এসি সার্কিট গণনা করার সময়, প্রতিরোধের ধারণার পরিবর্তে, "প্রতিবন্ধকতা" ধারণাটি চালু করা হয়। প্রতিবন্ধকতা Z অক্ষর দ্বারা চিহ্নিত করা হয়, এতে লোড R এর সক্রিয় প্রতিরোধ অন্তর্ভুক্ত রয়েছে_ক এবং প্রতিক্রিয়া এক্স (বা আর_r) এটি সাইনোসয়েডাল কারেন্টের আকৃতি (এবং অন্য কোনও ফর্মের স্রোত) এবং প্রবর্তক উপাদানগুলির পরামিতিগুলির পাশাপাশি স্যুইচিং আইনগুলির কারণে:

1. একটি ইন্ডাকটিভ সার্কিটে কারেন্ট তাৎক্ষণিকভাবে পরিবর্তন করতে পারে না।
2. একটি ক্যাপাসিট্যান্স সহ একটি সার্কিটের ভোল্টেজ তাত্ক্ষণিকভাবে পরিবর্তন করতে পারে না।

এইভাবে, কারেন্ট ভোল্টেজকে পিছিয়ে বা নেতৃত্ব দিতে শুরু করে এবং আপাত শক্তি সক্রিয় এবং প্রতিক্রিয়াশীল মধ্যে বিভক্ত হয়।

U=I/Z

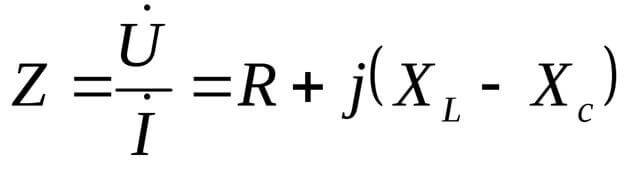
এক্স_এল এবং এক্স_গ লোডের প্রতিক্রিয়াশীল উপাদান।

এই বিষয়ে, cosФ মানটি চালু করা হয়েছে:

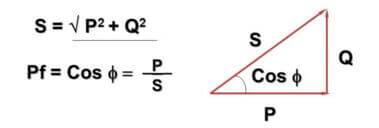
এখানে - Q - বিকল্প কারেন্ট এবং ইন্ডাকটিভ-ক্যাপাসিটিভ উপাদানের কারণে প্রতিক্রিয়াশীল শক্তি, P - সক্রিয় শক্তি (সক্রিয় উপাদানগুলিতে ছড়িয়ে পড়ে), S - আপাত শক্তি, cosФ - পাওয়ার ফ্যাক্টর।

আপনি হয়তো লক্ষ্য করেছেন যে সূত্র এবং এর উপস্থাপনাটি পিথাগোরিয়ান উপপাদ্যের সাথে ছেদ করে। এটি সত্য এবং কোণ Ф নির্ভর করে লোডের প্রতিক্রিয়াশীল উপাদানটি কত বড় তার উপর - এটি যত বড়, তত বড়।বাস্তবে, এটি এই সত্যের দিকে পরিচালিত করে যে নেটওয়ার্কে প্রকৃতপক্ষে প্রবাহিত কারেন্ট একটি পরিবারের মিটার দ্বারা বিবেচনা করা তুলনায় বেশি, যখন উদ্যোগগুলি সম্পূর্ণ শক্তির জন্য অর্থ প্রদান করে।

এই ক্ষেত্রে, প্রতিরোধ জটিল আকারে উপস্থাপিত হয়:

এখানে j হল একটি কাল্পনিক একক, যা সমীকরণের জটিল ফর্মের জন্য সাধারণ। কম সাধারণভাবে i হিসাবে উল্লেখ করা হয়, কিন্তু বৈদ্যুতিক প্রকৌশলে, বিকল্প কারেন্টের কার্যকরী মানও বোঝানো হয়, তাই, বিভ্রান্ত না হওয়ার জন্য, j ব্যবহার করা ভাল।

কাল্পনিক একক হল √-1। এটা যৌক্তিক যে বর্গ করার সময় এমন কোন সংখ্যা নেই, যার ফলে "-1" এর নেতিবাচক ফলাফল হতে পারে।

যখন ওহমের সূত্র ঘটে

আদর্শ পরিস্থিতি তৈরি করা সহজ নয়। এমনকি বিশুদ্ধ পরিবাহীতেও, বৈদ্যুতিক প্রতিরোধ তাপমাত্রার সাথে পরিবর্তিত হয়। এর হ্রাস ক্রিস্টাল জালির অণুগুলির কার্যকলাপকে হ্রাস করে, যা বিনামূল্যে চার্জের চলাচলকে সহজ করে। "হিমাঙ্ক" এর একটি নির্দিষ্ট স্তরে সুপারকন্ডাক্টিভিটির প্রভাব ঘটে। উত্তপ্ত হলে বিপরীত প্রভাব (পরিবাহিতা অবনতি) পরিলক্ষিত হয়।

একই সময়ে, ইলেক্ট্রোলাইট, ধাতু এবং নির্দিষ্ট ধরণের সিরামিক বর্তমান ঘনত্ব নির্বিশেষে বৈদ্যুতিক প্রতিরোধকে ধরে রাখে। একটি নির্দিষ্ট তাপমাত্রা শাসন বজায় রাখার সময় পরামিতিগুলির স্থিতিশীলতা অতিরিক্ত সংশোধন ছাড়াই ওহমের আইনের সূত্রগুলি প্রয়োগ করা সম্ভব করে তোলে।

অর্ধপরিবাহী পদার্থ এবং গ্যাস বিভিন্ন বৈদ্যুতিক প্রতিরোধের দ্বারা চিহ্নিত করা হয়। এই পরামিতি উল্লেখযোগ্যভাবে নিয়ন্ত্রণ ভলিউম বর্তমান তীব্রতা দ্বারা প্রভাবিত হয়. কর্মক্ষমতা বৈশিষ্ট্য গণনা করার জন্য, বিশেষ গণনা পদ্ধতি প্রয়োগ করা আবশ্যক।

যদি বিকল্প বর্তমান বিবেচনা করা হয়, গণনা পদ্ধতি সংশোধন করা হয়।এই ক্ষেত্রে, প্রতিক্রিয়াশীল উপাদানগুলির উপস্থিতি বিবেচনায় নিতে হবে। প্রতিরোধের প্রতিরোধী প্রকৃতির সাথে, ওহমের সূত্রের সূত্রের উপর ভিত্তি করে বিবেচনা করা গণনা প্রযুক্তি প্রয়োগ করা সম্ভব।

Kirchhoff এর আইন.

বিতরণ
বৈদ্যুতিক সার্কিটের শাখায় স্রোত
Kirchhoff এর প্রথম আইন মেনে চলে,
এবং বিভাগগুলির উপর চাপের বিতরণ
চেইন কির্চফের দ্বিতীয় আইন মেনে চলে।

Kirchhoff এর আইন
পাশাপাশি ওহমের সূত্র প্রধান
বৈদ্যুতিক সার্কিটের তত্ত্বে।

প্রথম
কিরচফের আইন:

বীজগণিত
নোডে স্রোতের যোগফল শূন্য:

_i
= 0 (19)

কোথায়
i
প্রদত্ত নোডে একত্রিত হওয়া শাখার সংখ্যা।

অর্থাৎ সমষ্টি
শাখায় স্রোত পর্যন্ত প্রসারিত হয়,
যা বিবেচনায় একত্রিত হয়
নোড

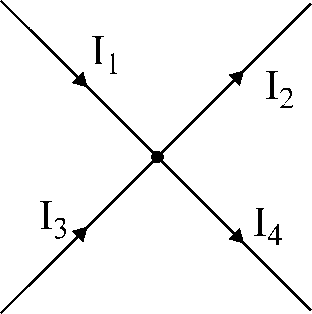
চিত্র.17। চিত্রণ
Kirchhoff এর প্রথম আইন.

সংখ্যা
সমীকরণ প্রথম অনুযায়ী সংকলিত
Kirchhoff এর সূত্র সূত্র দ্বারা নির্ধারিত হয়:

নুপ
= অনু
– 1,

কোথায়
অনু
বিবেচিত চেইনে নোডের সংখ্যা।

স্রোতের চিহ্ন
সমীকরণগুলি নির্বাচিতদের বিবেচনায় নেওয়া হয়
ইতিবাচক দিক। সাইন ইন
স্রোত একই যদি স্রোত একই হয়
এই আপেক্ষিক ভিত্তিক
নোড

উদাহরণ স্বরূপ,
চিত্র 17-এ দেখানো নোডের জন্য:
আমরা নোডে প্রবাহিত স্রোতগুলিতে চিহ্ন বরাদ্দ করি
"+", এবং নোড থেকে প্রবাহিত স্রোতের দিকে - লক্ষণ
«-».

তারপর সমীকরণ
Kirchhoff এর প্রথম আইন অনুযায়ী, এটি লিখিত হবে
তাই:

আমি₁
- আমি₂
+ আমি₃
- আমি₄
= 0.

সমীকরণ,
Kirchhoff এর প্রথম আইন অনুযায়ী সংকলিত,
নোড বলা হয়।

এই
আইন নোডে যে সত্য প্রকাশ করে
বৈদ্যুতিক চার্জ জমা হয় না
এবং খাওয়া হয় না। বৈদ্যুতিক পরিমাণ
সাইটে আসা চার্জ যোগফলের সমান
চার্জ এক এবং একই নোড ছেড়ে
একই সময়ের ব্যবধান।

দ্বিতীয়
কিরচফের আইন:

বীজগণিত
emf এর যোগফল যেকোনো ক্লোজ সার্কিটে
শৃঙ্খল ফলসের বীজগাণিতিক যোগফলের সমান
এই সার্কিটের উপাদানগুলিতে ভোল্টেজ:

Ui
= 
ই আই

IiRi = Ei(20)

কোথায়
i
- উপাদান সংখ্যা (প্রতিরোধ বা
ভোল্টেজের উৎস) বিবেচনা করা হয়
কনট্যুর

**সংখ্যা
দ্বিতীয় অনুযায়ী সমীকরণ সংকলিত
Kirchhoff এর সূত্র সূত্র দ্বারা নির্ধারিত হয়:

নুপ
= Nb
- অনু
+ 1 – Ned.s

কোথায়
এনবি
- বৈদ্যুতিক সার্কিটের শাখার সংখ্যা;

অনু
- নোডের সংখ্যা;

Ned.s.
আদর্শ emf উৎসের সংখ্যা।

চিত্র 18। চিত্রণ
Kirchhoff এর দ্বিতীয় আইন.

জন্য,
দ্বিতীয় আইনটি সঠিকভাবে লিখতে
একটি প্রদত্ত কনট্যুর জন্য Kirchhoff, অনুসরণ করে
নিম্নলিখিত নিয়ম মেনে চলুন:

1. নির্বিচারে
   কনট্যুর বাইপাসের দিক নির্বাচন করুন,
   উদাহরণস্বরূপ, ঘড়ির কাঁটার দিকে (চিত্র 18)।

2. emf
   এবং ভোল্টেজ ড্রপ যে ম্যাচ
   নির্বাচিত দিক দিয়ে দিক
   বাইপাস দিয়ে একটি অভিব্যক্তিতে লেখা হয়
   চিহ্ন "+"; যদি e.f.s. এবং ভোল্টেজ ড্রপ
   দিক মেলে না
   কনট্যুর, তারপর তারা একটি চিহ্ন দ্বারা পূর্বে হয়
   «-».

উদাহরণ স্বরূপ,
চিত্র 18 এর কনট্যুরের জন্য, Kirchhoff এর দ্বিতীয় আইন
নিম্নরূপ লেখা হবে:

উ₁
- ইউ₂
+ উ₃
=ই₁
- ই₃
- ই₄
(21)

সমীকরণ (20) হতে পারে
হিসাবে পুনরায় লিখুন:

 (Ui
- ই আই)
= 0 (22)

কোথায়
(ইউ
– ই)
- শাখায় উত্তেজনা।

অতএব,
Kirchhoff এর দ্বিতীয় আইন প্রণয়ন করা যেতে পারে
নিম্নলিখিত উপায়ে:

বীজগণিত
যেকোনো শাখায় ভোল্টেজের যোগফল
বন্ধ লুপ শূন্য।

সম্ভাব্য
পূর্বে আলোচিত চিত্রটি কাজ করে
দ্বিতীয়টির গ্রাফিকাল ব্যাখ্যা
Kirchhoff এর আইন.

টাস্ক নম্বর 1।

AT
চিত্র 1-এ সার্কিটকে স্রোত I দেওয়া হয়েছে₁
এবং আমি₃,
প্রতিরোধ এবং emf স্রোত নির্ধারণ করুন
আমি₄,
আমি₅,
আমি₆
; বিন্দুর মধ্যে ভোল্টেজ a
এবং খ
আমি যদি₁
= 10mA,
আমি₃
= -20 mA,
আর₄
= 5kOhm,
ই₅
= 20B,
আর₅
= 3kOhm,
ই₆
= 40B,
আর₆
= 2kOhm।

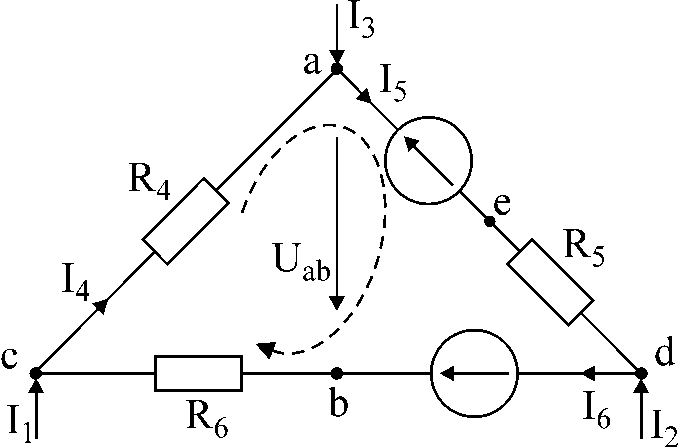
আকার 1

সমাধান:

1. একটি নির্দিষ্ট জন্য
   কনট্যুর, আমরা অনুযায়ী দুটি সমীকরণ রচনা করি
   Kirchhoff এর প্রথম আইন এবং একটি - অনুযায়ী
   দ্বিতীয় কনট্যুর দিক
   একটি তীর দ্বারা নির্দেশিত।

AT
সমাধানের ফলস্বরূপ আমরা পাই: I₆
= 0; আমি₄
= 10mA;
আমি₅
= -10mA

1. জিজ্ঞাসা
   পয়েন্টের মধ্যে ভোল্টেজের দিক
   ক
   এবং খ
   বিন্দু "a" থেকে
   বিন্দু "b"
   — ইউ_ab.
   এই ভোল্টেজটি সমীকরণ থেকে পাওয়া যাবে
   কির্চফের দ্বিতীয় আইন:

আমি₄আর₄
+ উ_ab
+ আমি₆আর₆
= 0

উ_ab
=- 50V।

টাস্ক নম্বর 2।

জন্য
চিত্র 2 এর ডায়াগ্রাম অনুযায়ী সমীকরণ আঁকুন
Kirchhoff এর আইন এবং অজানা নির্ধারণ
পয়েন্ট

প্রদত্ত:
আমি₁
= 20mA;
আমি₂
= 10mA

আর₁
= 5kOhm,
আর₃
= 4kOhm,
আর₄
= 6kOhm,
আর₅
= 2kOhm,
আর₆
= 4kΩ।

চিত্র 2

সমাধান:

নোডের সংখ্যা
সমীকরণ - 3, কনট্যুর সমীকরণের সংখ্যা
– 1.

মনে রাখবেন!
দ্বিতীয় অনুযায়ী সমীকরণ কম্পাইল করার সময়
Kirchhoff এর আইন, আমরা কনট্যুর নির্বাচন করুন, মধ্যে
যা বর্তমান উত্স অন্তর্ভুক্ত করে না।
কনট্যুরের দিকটি চিত্রে নির্দেশিত হয়েছে।

AT
এই সার্কিটের, শাখাগুলির স্রোত I₁
এবং আমি₂.
অজানা
স্রোত
আমি₃,
আমি₄,
আমি₅,
আমি₆.

সিদ্ধান্ত নিচ্ছে
সিস্টেম, আমরা পাই: আমি₃
= 13.75 mA;
আমি₄
= -3.75mA;
আমি₅
= 6.25mA;
আমি₆
= 16.25mA।

মৌলিক ধারণা

বৈদ্যুতিক প্রবাহ তখন প্রবাহিত হয় যখন একটি ক্লোজ সার্কিট ইলেকট্রনকে সার্কিটের একটি উচ্চ সম্ভাবনা থেকে নীচের দিকে যেতে দেয়। অন্য কথায়, কারেন্টের জন্য ইলেকট্রনগুলির একটি উত্স প্রয়োজন যাতে তাদের গতিশীল করার শক্তি থাকে, সেইসাথে তাদের ঋণাত্মক চার্জের প্রত্যাবর্তনের একটি বিন্দু, যা তাদের অভাব দ্বারা চিহ্নিত করা হয়। একটি শারীরিক ঘটনা হিসাবে, একটি সার্কিটে বর্তমান তিনটি মৌলিক পরিমাণ দ্বারা চিহ্নিত করা হয়:

• ভোল্টেজ, বৈদ্যুতিক একক বিশেষ;
• বর্তমান শক্তি;
• একটি পরিবাহীর প্রতিরোধ যার মাধ্যমে ইলেকট্রন চলাচল করে।

শক্তি এবং উত্তেজনা

বর্তমান শক্তি (I, অ্যাম্পিয়ারে পরিমাপ করা হয়) হল সময়ের প্রতি একক সার্কিটের একটি স্থানের মধ্য দিয়ে চলমান ইলেকট্রনের আয়তন (চার্জ)।অন্য কথায়, পরিমাপ I হল গতিশীল ইলেকট্রনের সংখ্যা নির্ণয়

এটা বোঝা গুরুত্বপূর্ণ যে শব্দটি শুধুমাত্র গতিবিধিকে বোঝায়: স্ট্যাটিক চার্জ, উদাহরণস্বরূপ, একটি সংযোগহীন ব্যাটারির টার্মিনালগুলিতে, I-এর একটি পরিমাপযোগ্য মান নেই। যে কারেন্ট এক দিকে প্রবাহিত হয় তাকে সরাসরি (DC) বলা হয় এবং পর্যায়ক্রমে দিক পরিবর্তন করাকে বলা হয় বিকল্প (AC)। ভোল্টেজকে চাপের মতো একটি ঘটনা বা অভিকর্ষের প্রভাবে বস্তুর সম্ভাব্য শক্তির পার্থক্য হিসাবে চিত্রিত করা যেতে পারে।

এই ভারসাম্যহীনতা তৈরি করার জন্য, আপনাকে প্রথমে শক্তি ব্যয় করতে হবে, যা উপযুক্ত পরিস্থিতিতে গতিতে উপলব্ধি করা হবে। উদাহরণস্বরূপ, উচ্চতা থেকে একটি লোড পড়ে গেলে, এটি উত্তোলনের জন্য কাজ করা হয়, গ্যালভানিক ব্যাটারিতে, টার্মিনালগুলিতে সম্ভাব্য পার্থক্য রাসায়নিক শক্তির রূপান্তরের কারণে তৈরি হয়, জেনারেটরে - এক্সপোজারের ফলস্বরূপ একটি ইলেক্ট্রোম্যাগনেটিক ক্ষেত্র

চাপকে চাপের মতো একটি ঘটনা দ্বারা বা মাধ্যাকর্ষণ শক্তির প্রভাবে বস্তুর সম্ভাব্য শক্তির পার্থক্য হিসাবে চিত্রিত করা যেতে পারে। এই ভারসাম্যহীনতা তৈরি করার জন্য, আপনাকে প্রথমে শক্তি ব্যয় করতে হবে, যা উপযুক্ত পরিস্থিতিতে গতিতে উপলব্ধি করা হবে। উদাহরণস্বরূপ, উচ্চতা থেকে একটি লোড পড়ে গেলে, এটি উত্তোলনের কাজটি উপলব্ধি করা হয়, গ্যালভানিক ব্যাটারিতে টার্মিনালগুলিতে সম্ভাব্য পার্থক্য রাসায়নিক শক্তির রূপান্তরের কারণে তৈরি হয়, জেনারেটরে - একটি এক্সপোজারের ফলস্বরূপ ইলেক্ট্রোম্যাগনেটিক ফিল্ড.

কন্ডাক্টর প্রতিরোধের

একটি সাধারণ পরিবাহী যতই ভাল হোক না কেন, এটি কখনই ইলেকট্রনকে তাদের চলাচলের কিছু প্রতিরোধ ছাড়াই অতিক্রম করতে দেয় না।যান্ত্রিক ঘর্ষণ এর একটি এনালগ হিসাবে প্রতিরোধ বিবেচনা করা সম্ভব, যদিও এই তুলনা নিখুঁত হবে না। যখন একটি পরিবাহীর মধ্য দিয়ে বিদ্যুৎ প্রবাহিত হয়, তখন কিছু সম্ভাব্য পার্থক্য তাপে রূপান্তরিত হয়, তাই প্রতিরোধক জুড়ে সর্বদা একটি ভোল্টেজ ড্রপ থাকবে। বৈদ্যুতিক হিটার, হেয়ার ড্রায়ার এবং অন্যান্য অনুরূপ ডিভাইসগুলি শুধুমাত্র তাপের আকারে বৈদ্যুতিক শক্তি নষ্ট করার জন্য ডিজাইন করা হয়েছে।

সরলীকৃত প্রতিরোধ (R হিসাবে চিহ্নিত) হল একটি পরিমাপ যা একটি সার্কিটে ইলেকট্রনের প্রবাহ কতটা মন্থর হয়। এটা ohms মধ্যে পরিমাপ করা হয়. একটি প্রতিরোধক বা অন্যান্য উপাদানের পরিবাহিতা দুটি বৈশিষ্ট্য দ্বারা নির্ধারিত হয়:

• জ্যামিতি;
• উপাদান.

আকৃতি অত্যন্ত গুরুত্বপূর্ণ, যেমন হাইড্রোলিক সাদৃশ্য থেকে স্পষ্ট: একটি দীর্ঘ এবং সরু পাইপের মাধ্যমে জল ঠেলে দেওয়া একটি ছোট এবং চওড়া দিয়ে জল ঠেলে দেওয়ার চেয়ে অনেক কঠিন। উপাদান একটি নিষ্পত্তিমূলক ভূমিকা পালন করে। উদাহরণস্বরূপ, তামার তারে ইলেকট্রন অবাধে চলাচল করতে পারে, কিন্তু রাবারের মতো অন্তরকগুলির মধ্য দিয়ে প্রবাহিত হতে পারে না, তাদের আকৃতি নির্বিশেষে। জ্যামিতি এবং উপাদান ছাড়াও, অন্যান্য কারণ রয়েছে যা পরিবাহিতাকে প্রভাবিত করে।

ওহমের আইনের ব্যাখ্যা

চার্জ চলাচল নিশ্চিত করতে, আপনাকে সার্কিটটি বন্ধ করতে হবে। অতিরিক্ত বিদ্যুতের অনুপস্থিতিতে, স্রোত দীর্ঘ সময়ের জন্য থাকতে পারে না। সম্ভাবনা দ্রুত সমান হয়ে যাবে। সার্কিটের অপারেটিং মোড বজায় রাখার জন্য, একটি অতিরিক্ত উত্স (জেনারেটর, ব্যাটারি) প্রয়োজন।

সম্পূর্ণ বর্তনীতে সমস্ত উপাদানের মোট বৈদ্যুতিক প্রতিরোধ ক্ষমতা থাকবে। সঠিক গণনার জন্য, কন্ডাক্টর, প্রতিরোধী উপাদান এবং একটি শক্তির উৎসের ক্ষতি বিবেচনা করা হয়।

একটি নির্দিষ্ট বর্তমান শক্তির জন্য কত ভোল্টেজ প্রয়োগ করতে হবে তা সূত্র দ্বারা গণনা করা হয়:

U=I*R.

একইভাবে, বিবেচিত সম্পর্কের সাহায্যে, সার্কিটের অন্যান্য পরামিতিগুলি নির্ধারিত হয়।

সমান্তরাল এবং সিরিয়াল সংযোগ

বৈদ্যুতিক ক্ষেত্রে, উপাদানগুলি হয় সিরিজে সংযুক্ত থাকে - একের পর এক, বা সমান্তরালে - এটি তখন হয় যখন একাধিক ইনপুট একটি বিন্দুতে সংযুক্ত থাকে এবং একই উপাদান থেকে আউটপুট অন্যটির সাথে সংযুক্ত থাকে।

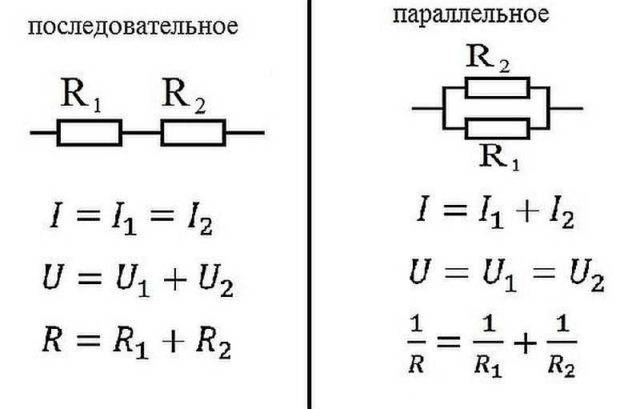
সমান্তরাল এবং সিরিজ সংযোগের জন্য ওহমের সূত্র

সিরিয়াল সংযোগ

কিভাবে ওহমের আইন এই ক্ষেত্রে কাজ করে? সিরিজে সংযুক্ত হলে, উপাদানের শৃঙ্খলের মধ্য দিয়ে প্রবাহিত কারেন্ট একই হবে। সিরিজে সংযুক্ত উপাদানগুলির সাথে একটি সার্কিটের একটি অংশের ভোল্টেজ প্রতিটি বিভাগে ভোল্টেজের যোগফল হিসাবে গণনা করা হয়। কিভাবে এই ব্যাখ্যা করা যেতে পারে? একটি উপাদানের মাধ্যমে তড়িৎ প্রবাহ হল চার্জের একটি অংশ থেকে অন্য অংশে স্থানান্তর। আমি বলতে চাচ্ছি, এটা কিছু কাজ. এই কাজের মাত্রা হল উত্তেজনা। এটি মানসিক চাপের শারীরিক অর্থ। যদি এটি পরিষ্কার হয়, আমরা এগিয়ে যাই।

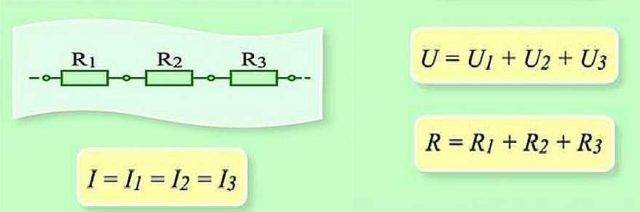
সার্কিটের এই বিভাগের সিরিয়াল সংযোগ এবং পরামিতি

সিরিজে সংযুক্ত হলে, প্রতিটি উপাদানের মাধ্যমে চার্জ স্থানান্তর করা প্রয়োজন। এবং প্রতিটি উপাদানে, এটি কাজের একটি নির্দিষ্ট "ভলিউম"। এবং চেইনের পুরো বিভাগে কাজের পরিমাণ খুঁজে পেতে, আপনাকে প্রতিটি উপাদানের কাজ যোগ করতে হবে। সুতরাং দেখা যাচ্ছে যে মোট ভোল্টেজ হল প্রতিটি উপাদানের ভোল্টেজের সমষ্টি।

একইভাবে - যোগের সাহায্যে - সার্কিট বিভাগের মোট প্রতিরোধও পাওয়া যায়। কিভাবে আপনি এটা কল্পনা করতে পারেন? উপাদানের শৃঙ্খলের মধ্য দিয়ে প্রবাহিত কারেন্ট ক্রমান্বয়ে সমস্ত প্রতিরোধকে অতিক্রম করে। একটার পর একটা. অর্থাৎ, তিনি যে প্রতিরোধকে অতিক্রম করেছেন তা খুঁজে বের করতে, প্রতিরোধগুলি যোগ করা প্রয়োজন। কমবেশি এরকম।গাণিতিক ডেরিভেশন আরও জটিল, এবং এই আইনের কার্যপ্রণালী বোঝা সহজ।

সমান্তরাল সংযোগ

একটি সমান্তরাল সংযোগ হল যখন কন্ডাক্টর / উপাদানগুলির শুরুগুলি এক বিন্দুতে একত্রিত হয় এবং অন্যটিতে তাদের প্রান্তগুলি সংযুক্ত থাকে। আমরা এই ধরনের যৌগগুলির জন্য বৈধ আইনগুলি ব্যাখ্যা করার চেষ্টা করব। কারেন্ট দিয়ে শুরু করা যাক। উপাদানগুলির সংযোগ বিন্দুতে কিছু মাত্রার একটি কারেন্ট সরবরাহ করা হয়। এটি পৃথক করে, সমস্ত কন্ডাক্টরের মধ্য দিয়ে প্রবাহিত হয়। এটি থেকে আমরা উপসংহারে পৌঁছেছি যে বিভাগে মোট কারেন্ট প্রতিটি উপাদানের বর্তমানের সমষ্টির সমান: I = I1 + I2 + I3।

এখন ভোল্টেজ জন্য. যদি ভোল্টেজ একটি চার্জ সরানোর কাজ হয়, তবে একটি চার্জ সরানোর জন্য যে কাজটি প্রয়োজন তা যে কোনও উপাদানে একই হবে। অর্থাৎ, প্রতিটি সমান্তরাল সংযুক্ত উপাদানের ভোল্টেজ একই হবে। U=U1=U2=U3. একটি চেইন বিভাগের জন্য ওহমের আইনের ব্যাখ্যার ক্ষেত্রে যেমন মজাদার এবং চাক্ষুষ নয়, তবে আপনি বুঝতে পারেন।

সমান্তরাল সংযোগের জন্য আইন

প্রতিরোধের জন্য, জিনিসগুলি একটু বেশি জটিল। চলুন পরিবাহিতা ধারণা চালু করা যাক. এটি এমন একটি বৈশিষ্ট্য যা নির্দেশ করে যে এই পরিবাহীর মধ্য দিয়ে একটি চার্জ পাস করা কতটা সহজ বা কঠিন। এটা স্পষ্ট যে প্রতিরোধ ক্ষমতা যত কম হবে, কারেন্ট পাস করা তত সহজ হবে। অতএব, পরিবাহিতা - জি - প্রতিরোধের পারস্পরিক হিসাবে গণনা করা হয়। সূত্রে, এটি এইরকম দেখায়: G = 1/R।

কেন আমরা পরিবাহিতা সম্পর্কে কথা বলছি? কারণ উপাদানগুলির সমান্তরাল সংযোগ সহ একটি বিভাগের মোট পরিবাহিতা প্রতিটি বিভাগের জন্য পরিবাহিতার সমষ্টির সমান। G = G1 + G2 + G3 - বোঝা সহজ। কারেন্ট কত সহজে সমান্তরাল উপাদানগুলির এই নোডকে অতিক্রম করবে তা প্রতিটি উপাদানের পরিবাহিতার উপর নির্ভর করে। সুতরাং দেখা যাচ্ছে যে তাদের ভাঁজ করা দরকার।

এখন আমরা প্রতিরোধের দিকে যেতে পারি।যেহেতু পরিবাহিতা হল প্রতিরোধের পারস্পরিক, আমরা নিম্নলিখিত সূত্র পেতে পারি: 1/R = 1/R1 + 1/R2 + 1/R3।

কি আমাদের একটি সমান্তরাল এবং সিরিয়াল সংযোগ দেয়?

তাত্ত্বিক জ্ঞান ভালো, কিন্তু বাস্তবে তা কীভাবে প্রয়োগ করবেন? যেকোনো ধরনের উপাদান সমান্তরাল এবং সিরিজে সংযুক্ত হতে পারে। কিন্তু আমরা রৈখিক উপাদানগুলিকে বর্ণনা করে শুধুমাত্র সহজতম সূত্রগুলি বিবেচনা করেছি। রৈখিক উপাদানগুলি হল প্রতিরোধ, যাকে "প্রতিরোধক"ও বলা হয়। সুতরাং আপনি যা শিখেছেন তা আপনি কীভাবে ব্যবহার করতে পারেন তা এখানে রয়েছে:

যদি কোন বৃহৎ-মূল্যের প্রতিরোধক উপলব্ধ না থাকে, তবে বেশ কয়েকটি ছোট থাকে, তবে সিরিজে বেশ কয়েকটি প্রতিরোধক সংযুক্ত করে কাঙ্ক্ষিত প্রতিরোধ পাওয়া যেতে পারে। আপনি দেখতে পারেন, এটি একটি দরকারী কৌশল।
ব্যাটারির আয়ু বাড়ানোর জন্য, তারা সমান্তরালভাবে সংযুক্ত হতে পারে। এই ক্ষেত্রে ভোল্টেজ, ওহমের আইন অনুসারে, একই থাকবে (আপনি একটি মাল্টিমিটার দিয়ে ভোল্টেজ পরিমাপ করে নিশ্চিত করতে পারেন)। এবং একটি দ্বৈত ব্যাটারির "জীবনকাল" দুটি উপাদানের তুলনায় অনেক বেশি হবে যা একে অপরকে প্রতিস্থাপন করবে

শুধু মনে রাখবেন: একই সম্ভাবনার সাথে শুধুমাত্র পাওয়ার সাপ্লাই সমান্তরালভাবে সংযুক্ত করা যেতে পারে। যে, একটি মৃত এবং একটি নতুন ব্যাটারি সংযুক্ত করা যাবে না.

আপনি যদি এখনও সংযোগ করেন, তাহলে যে ব্যাটারির চার্জ বেশি থাকে সেটি কম চার্জে চার্জ হতে থাকে। ফলস্বরূপ, তাদের মোট চার্জ কম মূল্যে নেমে যাবে।

সাধারণভাবে, এই যৌগগুলির জন্য এইগুলি সবচেয়ে সাধারণ ব্যবহার।

আদর্শ EMF উৎস

ইলেক্ট্রোমোটিভ ফোর্স (E) হল একটি ভৌত ​​পরিমাণ যা চার্জ বাহকের ক্লোজ সার্কিটে চলাচলের উপর বহিরাগত শক্তির প্রভাবের মাত্রা নির্ধারণ করে। অন্য কথায়, কন্ডাক্টরের মধ্য দিয়ে কারেন্ট কতটা জোরালোভাবে প্রবাহিত হয় তা নির্ভর করবে EMF-এর উপর।

এই ধরনের বোধগম্য ঘটনা ব্যাখ্যা করার সময়, গার্হস্থ্য বিদ্যালয়ের শিক্ষকরা জলবাহী উপমাগুলির পদ্ধতিতে ফিরে যেতে পছন্দ করেন। যদি একটি কন্ডাকটর একটি পাইপ হয়, এবং বৈদ্যুতিক প্রবাহ হল এটির মধ্য দিয়ে প্রবাহিত জলের পরিমাণ, তাহলে EMF হল সেই চাপ যা একটি পাম্প তরল পাম্প করার জন্য তৈরি হয়।

ইলেক্ট্রোমোটিভ ফোর্স শব্দটি ভোল্টেজের মতো ধারণার সাথে সম্পর্কিত। সে, EMF, ভোল্টেও পরিমাপ করা হয় (ইউনিট - "V")। প্রতিটি শক্তির উত্স, তা একটি ব্যাটারি, একটি জেনারেটর বা একটি সৌর প্যানেল, তার নিজস্ব ইলেক্ট্রোমোটিভ শক্তি আছে। প্রায়শই এই EMF আউটপুট ভোল্টেজ (U) এর কাছাকাছি থাকে, তবে সর্বদা এটির থেকে কিছুটা কম। এটি উৎসের অভ্যন্তরীণ প্রতিরোধের কারণে ঘটে, যার উপর ভোল্টেজ অনিবার্যভাবে নেমে যায়।

এই কারণে, EMF-এর আদর্শ উৎসটি বরং একটি বিমূর্ত ধারণা বা একটি ভৌত ​​মডেল যার বাস্তব জগতে কোনো স্থান নেই, কারণ ব্যাটারি রিনের অভ্যন্তরীণ প্রতিরোধ ক্ষমতা খুব কম হলেও, এখনও পরম শূন্য থেকে ভিন্ন।

emf এর আদর্শ এবং বাস্তব উৎস

ডিফারেনশিয়াল আকারে

সূত্রটি প্রায়শই একটি ডিফারেনশিয়াল আকারে উপস্থাপিত হয়, যেহেতু কন্ডাকটরটি সাধারণত একজাতীয় হয় না এবং এটিকে সম্ভাব্য ক্ষুদ্রতম বিভাগে বিভক্ত করা প্রয়োজন। এর মধ্য দিয়ে প্রবাহিত কারেন্টটি মাত্রা এবং দিকনির্দেশের সাথে যুক্ত, তাই এটি একটি স্কেলার পরিমাণ হিসাবে বিবেচিত হয়। যখনই একটি তারের মাধ্যমে ফলিত কারেন্ট খুঁজে পাওয়া যায়, তখন সমস্ত পৃথক স্রোতের বীজগণিতিক যোগফল নেওয়া হয়। যেহেতু এই নিয়ম শুধুমাত্র স্কেলার পরিমাণে প্রযোজ্য, তাই কারেন্টকেও স্কেলার পরিমাণ হিসাবে নেওয়া হয়। এটি জানা যায় যে বর্তমান dI = jdS বিভাগটি অতিক্রম করে। এটির ভোল্টেজটি Edl এর সমান, তারপরে একটি ধ্রুবক ক্রস বিভাগ এবং সমান দৈর্ঘ্য সহ একটি তারের জন্য, অনুপাতটি সত্য হবে:

ডিফারেনশিয়াল ফর্ম

অতএব, ভেক্টর আকারে কারেন্টের প্রকাশ হবে: j = E।

গুরুত্বপূর্ণ ! ধাতব পরিবাহীর ক্ষেত্রে, ক্রমবর্ধমান তাপমাত্রার সাথে পরিবাহিতা হ্রাস পায়, যখন অর্ধপরিবাহীর ক্ষেত্রে এটি বৃদ্ধি পায়। ওমভের আইন কঠোর আনুপাতিকতা প্রদর্শন করে না

পরম শূন্যের কাছাকাছি তাপমাত্রায় ধাতু এবং সংকর ধাতুগুলির একটি বৃহৎ গোষ্ঠীর প্রতিরোধ অদৃশ্য হয়ে যায় এবং প্রক্রিয়াটিকে বলা হয় অতিপরিবাহীতা।